quadratrix

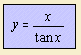
The quadratrix can be defined as the intersection of two moving lines. The first line rotates (for example counter clockwise), the second line moves along (for example in the direction of the positive y-axis). Both movements are with constant velocity. Can you imagine?

It was the Greek Hippias of Ellias (or Elis), who used the curve (about 420 BC) for the trisection of an angle. So that the curve is also called the quadratrix of Hippias.
This Hippias was a traveller, being a statesman and a philosopher; Plato describes him as a vain and boastful person.

Deinostratos (about 350 BC) and Nicomedes used the curve ¹⁾ while working on the problem of squaring the circle. That where the curve's name is from.

Funny is that the curve's equation can be expressed in the mixed Cartesian-polar form: y = π.

It is the polar inverse of the cochleoid.

notes

1) according to Pappos.

2) See at the Archimedes' spiral for a short exposure on these Classical problems.