|
Make your own painting with this circle applet:
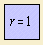
The circle
1) is the ellipse whose axes are equal
in length.
The ellipse is the linear distortion of the
circle, e.g. emerging when looking at a circle from an angle.
The circle is the curve for which the curvature is a
constant: dφ/ds = 1.
Half of a circle is called a semicircle.
 Because of
its symmetry
the circle is considered as the perfect shape. It is the symbol for the total symmetry of
the divine (sic!). The Greek scholar Proclus (500 AC) wrote: "the circle is the
first, the simplest and most perfect form". As Christian symbol it represents
eternity, and the sleeping eye of God (Genesis 1:2).
An anonymous poet wrote:
oh, the Circle, she is so divine
her curve is round, unlike the line.
The Dutch artist Toon Hermans said:
I have wandered a lot and I found:
most good things are round:
the breast of a mother, a tuba, plums and cherry flan.
More rational the circle can be described as the ellipse, where the two foci
coincide. Or
as the collection of points with equal distance to a (center) point. At the top of this
page we see the polar equation of a unity circle
(or unit circle) 2) with radius 1 and as center the
origin.
This definition - which gives the essence of the circle - was already formulated by Euclid
(300 BC) in book III of his 'Elements'. That's why you can draw the curve with a pair of
compasses. The circle's form
remains intact while turning, what makes her very useful as lid for closing
jars. And also
for a watch with turning hands. The diameter of a screw is a circle too. But man
got the greatest
advantage from the insight that for a wheel of a cart not the square, but
the circle is the most suitable form. So the study of the circle goes back beyond
recorded history.
The first mathematician to be attributed theorems about circles was the Greek Thales
(650 BC).
Creating a sand castle, you ought to know that, with a given amount of surface, on the
form of a circle the highest sand tower can be constructed. A corresponding quality have
circular drum skins: with a given amount of skin they produce the lowest
frequency.
Another quite practical advantage of the circle is that it has no sharp edges, and
distributes the pressure from the inside evenly. That's why the intersection of a
hose-pipe has the form of a circle.
You can cut from your circular birthday cake a part, in one straight line
(chord). This
piece is called a circle segment. More common is to divide the cake from the
middle in some circle segments. Those wedges can nicely demonstrate the distribution of a
variable: a circle diagram.
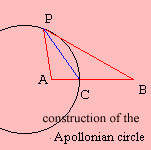 The Apollonian
circle (or Apollonius circle)
can be constructed for a segment AB, whose points P have a ratio PA/PB
= k. When C is the point on AB for which AC/CB = k, it is easy to see that the circle
views the segments AC and BC under equal angles 3).
Paris Pamfilos' Isoptikon (796 kB) is a tool for
for simply drawing these circles. Generalization of this circle leads to the Apollonian cubic. The Apollonian circle has been studied
by Apollonius of Perga.
There are three other definitions for the Apollonius circle:
-
one of the eight circles that are tangent to three given
circles
-
one of the three circles that pass through a vertex and the
isodynamic points of a triangle
-
the circle that touches the three excircles of a triangle
and encompasses them
Already centuries before the Christian era mathematicians tried to calculate the area of
the circle 4). The discovery of this area
being proportional to the power of the radius, led to the effort to determine this
proportional constant (pi) as exactly as possible 5).
This question is related to the problem of the circle's quadrature: to construct a square
with the same area as a given circle. The first to deal with this question was Anaxagoras
(540 BC). As proverb 'squaring a circle' has the meaning of
trying something that is completely impossible.
A nice quality of the circle is shown in the story of Dido: this Phoenician
princess escapes her town Tyrus (in today's Lebanon), after her brother (king
Pygmalion)
killed her husband. She went to the north coast of Africa, where she aimed to settle a new
town. Dido wanted to buy land from king Jarbas of Namibia, the emperor at that place.
Whether she didn't want to spend a lot of money, or Jarbas didn't want settlements is not
clear. But the fact is that they agreed that Dido could get as much land as the skin of an
ox could cover. Luckily for her the queen was so clever to cut the skin in a long rope
(probably more than a mile in length) and to lay this in the form of a circle, enclosing
as much land as possible. This meant the settlement of the city of Cartage (814
BC). The
story illustrates the circle being the solution of the isoperimetric problem 6). This
problem, one of the oldest problems
in variation calculus, was already known by the old Greek. So did Pappus, a Greek scholar
from Alexandria (300 BC), already have a good understanding of the problem. In this
knowledge, he followed a book of Zenodorus (180 BC) 7).
Some relations of the circle with other curves are the following:
Sometimes the forces of nature cause circular motions. Drops of fat in the soup have
the form of a circle: the circle gives the situation of the least potential energy, for
the existing molecular forces.
Object do not move in a circle by their selves, they need a force that is directed to the
middle of that circle. Examples of such motions are to be seen in the sport of throwing
away a iron shot with a cable, and the movement you make yourself, by standing on the
rotating earth. When a point moves with constant velocity in a circular orbit, one speaks
of a harmonic oscillation 8).
The old Greek had the idea the celestial bodies moving in a constant circular motion, with
the earth in the center of those orbits. To fit this model with the experimental facts of
the planetary movements, the condition of the earth in the circle's center was omitted. And also combinations of circular motions were proposed: epicycles.
These astronomical theories persisted until mid 17th century.
Another celestial phenomenon consisting of circles is the shape of the lighted moon, a
combination of two circles. Seen from the earth, one side of that moon is illuminated by
the sun.
The brilliant physician Einstein gave his name to the Einstein circles, an
optical (relativistic) effect when two solar objects are placed exactly in line behind
each other (for an earthly observer). It's in fact an extra solar gravitational lens, and
the first observation occurred in 1987.
So the circle is a
well-known form in our world, and we can find her back in a lot words and expressions.
Sometimes the round form is used: the circle scissors who succeeds to cut round pieces;
the round form of the circus ring. The circle of Willis is a circular spot on the
human body where inner en outer temperature are being compared. And the Vieth-Muller
circle is a special case of the horopter.
But often the emphasis is on the turning movement. In the case of a circular saw the
moment is exactly in a circle, but in words as circular, circuit, circulation only a
closed ring remains. In expressions about circles the meaning refers often to that
movement: in a circular argument that what is to be proven, is used as given, so that the
proof looses it's value. In a circular definition we see two definitions, who point to
each other. In a vicious circle one comes once again back in it's starting position.
During the 19th century it was a popular occupation in geometry to construct all sorts of
circles inside a triangle. Relatively easy to imagine are:
- outside circle: circle through the vertices of the triangle
- incircle, inside circle or inscribed circle:
largest circle that fits completely inside the triangle
- excircle or touching circle: extend two vertices of a triangle, and construct an outer circle that touches the vertices as well as the other triangle's vertex.
Less common circles are:
I save the reader the details of the former three circles.
The Villarceau circles are two circles formed by cutting a torus diagonally through the center at a correct angle.
They are named after the French astronomer and mathematician Yvon Villarceau (1813–1883).
The circles have also been studied by Mannheim (1903) and Schoelcher (1891).
See the animation at wikipedia.
The circle has a conchoid: the conchoid
of a circle.
Curves composed of more than one circle can be found on the more
circles page.
notes
1) In Italian: circulo or cerchio.
2) When the radius has the value zero, the circle is reduced to a single point, what is
called a point circle.
3) Line PC bisects the angle APB.
4) The Egypt (1900 BC), the Mesopotamian (1700 BC), the Chinese and the Indian (500
BC). Struik 1977 chapter 2.
5) The value of π is about 3,14159.
6) Iso (Gr.) = equal, perimetron (Gr.) = perimeter, contour.
7) The ultimate proof was given not earlier than in the second part of the 19th century, by Weierstrass.
8) To be compared with the sine.
|
