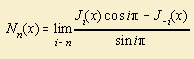Bessel function

The Bessel function is the solution of the Bessel differential equation:

The functions are found for systems with cylindrical symmetry.
Bessel was a mathematician who lived from 1784 to 1846.

There are two linear independent solutions:

• Bessel function of the first kind
• Bessel function of the second kind
  

Sometimes the Bessel function is called the cylinder function.
More common is to reserve this name for the three-dimensional cylinder function. However, the Fourier transform of this 3d function, is a Bessel function of the first kind (of first order).

Bessel function of the first kind

When speaking of the Bessel function, normally the Bessel function of the first kind order n, J_n(x), is meant.

It can be written as an infinite polynomial with terms derived from the gamma function:

It is found when solving wave equations. For instance, in the case of a wave equation on a membrane ¹⁾, the solution is a Bessel function of integer order (a). For a circular membrane the standing wave solution can be expressed as a Bessel function, under the condition that J_n(R)=0, where R is the distance from the origin to the rim of the membrane.
We see three standing wave animations: the first and second part of the order 0 function, and the first part of the order 1 function.

The Bessel function of the first kind and order 0 can occur when you wiggle an (idealized) chain, fixed at one side:

The Bessel functions J_n+½(x) are found in the definition of spherical Bessel functions.
These functions can be expressed in sine and cosine terms.
So can be found that:
and

From the Bessel function of the first kind two Kelvin functions ber_n(x) and bei_n(x) can be derived, in the following way:

ber_n(x) + i bei_n(x) = e^nπi J_n(x e ^{- πi/4})

Bessel function of the second kind

The Bessel function of the second kind of order n, Y_n(x), is also called the Weber function or the Neumann function N_n(x).

it can be written as an infinite polynomial with terms derived from the gamma function:

The Bessel function of the third kind or Hankel function H_n(x) is a (complex) combination of the two solutions: the real part is the Bessel function of the first kind, the complex part the Bessel function of the second kind.

notes

1)