Lerch transcendent

where the terms with i + a = 0 are excluded. 

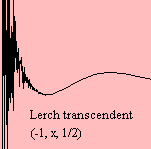The Lerch transcendent Φ(x₁, x₂, a) is a generalization of the polylogarithm (regarding x₁) and the (generalized) zeta function (regarding x₂).

Many infinite sums (of reciprocal powers) can expressed as a Lerch transcendent, for instance the Catalan beta function.
The function is also related to integrals of the Fermi-Dirac distribution. And it is used to evaluate some series in number theory (Dirichlet L-series).