kampyle of Eudoxus

This quartic curve has been studied by Eudoxus of Cnide (406-355 BC), an astronomer, philosopher and mathematician who was a pupil of Plato.

Eudoxus worked on the curve in relation to the classical problem of the duplication of the cube.
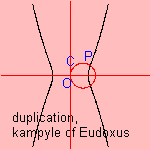
Let there be a circle C through O with radius √1/2, which cuts the kampyle in P.
Then OP has as length ³√2

In polar coordinates the curve can be written as r = cos ^-2 φ.

The kampyle ¹⁾ is also named Clairaut's curve.

And the kampyle is:

• the radial of the catenary
• the inverse of the double egg
  

Its Cartesian equation resembles the equation of the lemniscate of Gerono.

notes

1) Kampyle (Gr.) = curved