piriform

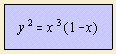
This curve has a form resembling a pear ¹⁾, why it is also called pear-shaped quartic or pear-shaped curve.
The first to study the curve was the French mathematician G. de Longchamps (1886).

The curve is defined in a rather complex way, in the following steps:

• let there be a circle C with a point O on it
• let there be a line l, perpendicular to the diameter of the circle through O
• now, draw an arbitrary line m through O, crossing l in P
• draw a line n perpendicular to l through P, crossing C in points Q
• then, draw a line o parallel to l through Q
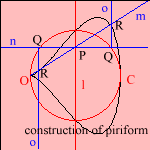
• now the curve is formed by the points R that are intersection of the lines o and the arbitrary line m

Could you follow me? If not, take a look at the picture.

In fact, the given formula is a (linear) generalization of the curve. The construction is only valid for the curve when the constant 1 is replaced by the 2.

The piriform has as parameter equation:

The curve is also called the pegtop, it is easy to see why.

In your throat there is a place where pieces of food can be stuck, e.g. a fish bone. This pit is called the piriform fossa ²⁾.

The curve can be generalized to the teardrop curve.

notes