|

 The word
'parabola' refers
to the parallelism of the conic section and the tangent of the conic mantle. Also
the parable 1) has been derived
from the Greek 'parabole'. The word
'parabola' refers
to the parallelism of the conic section and the tangent of the conic mantle. Also
the parable 1) has been derived
from the Greek 'parabole'.
The parabola can be seen as an ellipse with one focus in
infinity. This means that a parallel light bundle in a parabolic mirror will come together
in one point. It had been told that Archimedes did use a parabolic mirror in
warfare. It was during the siege of Syracuse (214 - 212 BC) by the Romans, that Archimedes
constructed reflecting plates in about the form of a parabola. These plates were used to
converge the sunlight onto the Roman ships, and put them in fire. Though this event is
discussed by some historians, recently the feasibility of Archimedes' plan has been proved
2).
Other technological parabola shaped objects are the parabolic microphone and the parabolic
antenna, used to focus sound and electromagnetic waves, respectively.
Menaichmos (350 BC) found the parabola while trying to duplicate
the cube: finding a cube with an area twice that of a given cube 3). In fact he tried to solve the equation x3
= 2. Menaichmos solved the equation as the intersection of the parabolas y = x2
and x = ½ y2.
Euclid (about 300 BC) wrote about the parabola in his treatise 'Conic Sections' (lost).
Apollonius (200 BC) also wrote about the parabola, in four books with the same name, probably using Euclid's work.
He was the one that gave the parabola its name.
Hypatia (355-415), the first known female mathematician, wrote 'on the conics of Apollonius',
a popularization of the work of Appolonius. After Hypatia, it seems that the conics were neglected
until the seventeenth century.
René Descartes (1596-1650) chose the parabola, in his work 'La Géométrie' (1637), to illustrate his work on analytic geometry.
Blaise Pascal (1623-1662) saw the curve as the projection of a circle.
Pierre de Fermat wrote in 1636 in a letter to Roberval that he had found the generalization of the curve,
that has later been given the name of parabola of Fermat, 7 years earlier.
As you see, the parabola is one of the most studied curves.
 In the parabola curve the parabola
(with its vertex oriented downwards) is being repeated infinitely.
In the parabola curve the parabola
(with its vertex oriented downwards) is being repeated infinitely.
Some properties of the parabola:
Besides, the following curves can be derived from the parabola:
Pedals of the parabola are given by:
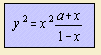
The Italian Luca Valerio determined the
area of a parabola, in 1606; is was called the quadrature of the parabola. But it was Archimedes who
first found the value of this area. In his work "Quadrature of a Parabola" he
formulated the area as 2/3 from the product of the base and the height of the parabolic
sector 3).
At the end of the the Middle Ages the cannon came into use on the
battlefield. Therefore it was important to predict the exact location where the
projectile would land. Many scientists tried to answer this question, and it was
Galileo Galilei (1564-1642) who found the relation as first.
That the trajectory of a projectile - neglecting effects
of friction - has the form of a parabola, can easily be understood as follows: the x coordinate is proportional to the elapsed time,
the y coordinate quadratic (as result of the constant gravitation force).
As a matter of fact, this relation was in the 15th century already known as the 'square law'.
When the air friction is taken into account, a braked
parabola emerges, what in fact is a kind of exponential curve.
The 'parabolic velocity' is the minimum velocity to escape from (the gravity forces of) a
celestial object.
And an arch (e.g. of stone) is called parabolic when its shape has the form of a ....
 Now it's time for an experiment: hang on a horizontal chord some lamps, at equal
distances. Neglecting the weight of the chord compared to the lamps, the hanging points of
the lamp form a parabola 4). This form is
independent of the weight of the lamps, and also of the distance between the lamps. In the
case of a chord without lamps, instead of a parabola, a catenary is formed.
Now it's time for an experiment: hang on a horizontal chord some lamps, at equal
distances. Neglecting the weight of the chord compared to the lamps, the hanging points of
the lamp form a parabola 4). This form is
independent of the weight of the lamps, and also of the distance between the lamps. In the
case of a chord without lamps, instead of a parabola, a catenary is formed.
Jungius (1669) proved that Galileo was wrong to state this curve
being a parabola.
On holidays at the Dutch North Sea beach, you can see dunes in the form of a parabola
(parabola dune), formed by the sand, thrown by the wind, but hold by the dune plants.
When experimenting, one will often encounter quadratic relations between variables. So is
the kinetic energy of a body proportional with the square velocity. In another branch of
mathematics we find the iterated parabola, studied for the first time (in the 60s) by Myrberg.
In the case of convergence one speaks of an attractor. And the warmth
equation, a partial second order differential equation, is also called the parabolic
differential equation. Reason is the similarity between the relations 5).
Rudolph Marcus used parabolae (in 1956) to explain the rates of electron transfer reactions.
His Marcus theory states that the reorganization energy for chemical redox reactions is a parabolic function of the unit charge of this hypothetical transfer.
Marcus won the the Nobel Prize in Chemistry in 1992.
notes
1) Para = next to, bole (Gr.) = throw, parabole = what is thrown next
to (to compare).
2) Mueller 1985 p. 111.
3) one was looking for a cube with contains twice the volume of a given cube: Waerden 1950 p. 88.
4) with thanks to Chris Rorres
(Drexel University).
5) This follows from setting to zero of the force momentum, working on the lowest point
of the chord.
6) . .
|







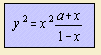
 The word
'parabola' refers
to the parallelism of the conic section and the tangent of the conic mantle. Also
the parable
The word
'parabola' refers
to the parallelism of the conic section and the tangent of the conic mantle. Also
the parable  In the
In the  Now it's time for an experiment: hang on a horizontal chord some lamps, at equal
distances. Neglecting the weight of the chord compared to the lamps, the hanging points of
the lamp form a parabola
Now it's time for an experiment: hang on a horizontal chord some lamps, at equal
distances. Neglecting the weight of the chord compared to the lamps, the hanging points of
the lamp form a parabola