exponential function

The variable x in the equation is called the 'exponent', the function is called the exponential function. The oldest exponential series is: 1, 2, 4, 8 and so on. There is an old legend about a scholar who could choose his own reward for some job. He asked to place grains of corn on a chess board, starting with one, on each field the double amount of the former...
With the Euler number e ¹⁾ as base of the power, the function is the natural exponential function exp(x), sometimes abbreviated as exponential function. For other values of the base of the power the function is a general exponential function.

The inverse of the exponential function is the logarithmic function or logarithm. This general logarithm is written as y = ^a log(x) or y = log_a(x).
For e as the base of the logarithm the curve is called the natural logarithm ln(x) ²⁾. Her derivative is the hyperbola y=1/x. The natural logarithm is sometimes called the Napierian logarithm, but these two are slightly different ³⁾. John Napier (1550-1617), a Scottish baron from Merchiston, was the first to relate the geometric series and the arithmetic series. For this purpose he uses the logarithm function.
For 10 as the base of the logarithm we've got the common logarithm log(x), also called Briggs' logarithm or Briggian logarithm. Henry Briggs (1561-1631) was an English mathematician, an admirer of Napier, who wrote the natural logarithm in its modern form (1624). It is common to measure the volume of sound in decibels, which has been defined as the ¹⁰log of the proportion of the measured sound pressure to the atmospheric pressure.
For 2 as the base of the logarithm the binary logarithm lb(x) is the case.
In relation to the logarithm, the exponential function can be denoted as inverse logarithm or antilogarithm.

The logarithm can be generalized as the polylogarithm.

In ancient times, when calculators and computers were uncommon (or not existent at all), many calculations were done with the help of  logarithmic derivations. Operations as multiplying, dividing or raising to a power can be simplified to the adding and subtracting of logarithms by use or relations as log ab = log a + log b and log a^k = k log a.
You can use a slide-rule with a logarithmic scale, on two parts, one movable. By pulling out the movable part a logarithmic addition or subtraction can be made. The result can be seen at once. When more precise resulted are necessary, you can use logarithmic tables, with the desired accuracy. Ciphering is now looking up various logarithmic values, subtracting or adding, and looking up the final result in the logarithmic table.

In the time of the logarithmic tables the cologarithm was used to prevent negative results. The function has been defined as: colog(x) = ¹⁰ log(1/x).

When experimentally testing an exponential relation between variables, it makes sense to display the results on logarithmic paper. This is squared paper where one of the two axes has a logarithmic (semi logarithmic) scale. When a straight line emerges, the exponential relation has been confirmed. From the angle with the x-axis the exponent can be derived. Because ^blogz = ^clogz / ^clogb, different bases of power are related with a constant factor. So one logarithmic choice satisfies.
When using two logarithmic (double logarithmic) axes, a power relation between two variables - like y = x ^a - can be tested.

Consider that something grows, proportional with time as well with quantity. In such a simple model growth takes place exponentially as function of the time. This can also be formulated as dy = a y dt, so y' = a y and y(t) = y(0) e ^at.
That's why the curve is also called growth curve. The exponential function grows faster than each polynomial (in x), and we can prove that :

Many physical processes pass away as a (natural) exponential function of the time. In many cases there is a negative exponent, a phenomenon gradually approaches some equilibrium.
For radioactive decay the constant in the exponent is determined by the kind of isotope. For the process of absorption of light the constant is called the absorption coefficient. For a closed electrical circuit with voltage V, resistance R and capacity (of capacitor) C the charge on the capacitor approaches asymptotically to C V ⁴⁾.
We go on: for a turbulent flow you can describe the distance between points in the flow as increasing exponentially with time.
And in ionic crystals there exists, except for an attractive Coulomb force, also a repellent force. A force for which the potential is an exponential function of the distance (with negative exponent).
For the high water for the Dutch coast you can graph how many times a certain height has been reached. This curve is also a (negative) exponential curve, according wait time theory.

The law of Euler gives the relationship between the exponential and the trigonometric functions: e^ix = cosx + i sinx, so that the following wonderful relationship holds: e^πi + 1 = 0.

notes

1) The Euler number e is about 2.71828. She can be defined in different ways, for instance as:
or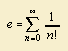

Because of his many contributions to mathematics it is quite rightly that the number e has been named tot Euler.

2) Sometimes the natural logarithm is written as log(x).

3) For the Napierian logarithm y = Neplog(x) the relation between x and y is as follows:
,  Struik 1977 p. 113.

4) Solution of the differential equation R Q'(t) + Q(t) / C = V is: