Mandelbrot set

where f is a Mandelbrot lemniscate

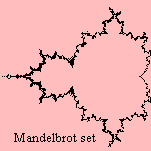The Mandelbrot set is one of the most popular fractals, on many places on the internet pictures (often colored) of the curve are to be seen.
The curve is a generalization of the bifurcation to the complex numbers.
The boundary of the set is very complex, and while enlarging and enlarging this part of the picture, again and again different beautiful structures are conveyed. In some parts miniature Mandelbrot set formed Mandelbrot baby's are to be seen.

Before Mandelbrot already the Hungarian mathematician Riesz (1952) posed questions related tot the Mandelbrot set. In 1978 Brooks and Matelski made the first computer graphics of the curve. Adrien Douady and John Hubbard studied the curve, they proved that the set is connected, and named it to Mandelbrot.
In 1994 it was Shishikura who proved the (Hausdorff) dimension of the curve being 2.
It is not yet known whether the curve is path-connected.

The main part of the curve, on the right, has the form of a cardioid; the part on the right has the form of a circle.