|
 |
 |
 |
 |
 |
 |
pedal curve |
main |
Given a curve C1 and a
(pedal) point O, construct
for each tangent l of C1 a point P, for which OP is perpendicular to the tangent. The
collection of points P forms a curve C2, the (positive)
pedal of C1 (with respect to the pedal point).
When C1 is given by (x, y) = (f(t), g(t)), and we translate C1 in such a way that the
pedal point is the origin, then C2 has the form:
Two curves are invariant for making a pedal:
- the sinusoidal spiral (pedal is unequal)
- the pedal of a logarithmic spiral is an equal logarithmic spiral
The pedal of the parabola is the curve
given by the equation:
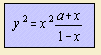
| a | pedal point | pedal of the parabola |
| 0 | vertex | cissoid (of Diocles) |
| 1 | foot of - intersection of axis and - directrix | (right) strophoid |
| 3 | reflection of focus in directrix | trisectrix of MacLaurin |
| - | on directrix | oblique strophoid |
| - | focus | line |
Some other pedals are:
| curve | pedal point | pedal |
| astroid | center | quadrifolium |
| cardioid | cusp | Cayley's sextic |
| circle | any point | limaçon |
| on circle | cardioid | |
| cissoid (of Diocles) | focus | cardioid |
| deltoid | cusp | simple folium |
| vertex | regular bifolium | |
| center | trifolium | |
| on the curve | bifolium | |
| ellipse | focus | circle |
| epicycloid | center | rhodonea |
| equiangular spiral | pole | equiangular spiral |
| hyperbola | focus | circle |
| rectangular hyperbola | center | lemniscate |
| hypocycloid | center | rhodonea |
| involute of a circle | center | Archimedes' spiral |
| line | any point | point |
| parabola | focus | line |
| on directrix | strophoid | |
| center of directrix | right strophoid | |
| reflection of focus by directrix | trisectrix of Maclaurin | |
| vertex | cissoid | |
| sinusoidal spiral | pole | sinusoidal spiral |
| Talbot's curve | center | ellipse |
| Tschirnhausen's cubic | focus | parabola |
The reverse operation of making a pedal is to construct from each point P of C2 a line l
that is perpendicular to OP. The lines l together form an envelope of the curve C1. Now we
call C1 the negative pedal 1)
of C2. When C1 is
a pedal of C2, then C2 is the negative pedal of C1.
Because of this definition, the curve is in fact also an orthocaustic:
the orthocaustic of a curve C1 (with respect to a point O) is the envelope of
the perpendiculars of P on OP (P on C1).
Instead of tangents to a curve we can consider normals to that curve. This pedal curve is
called the normal pedal curve.
MacLaurin was the first author to investigate pedal curves (1718).
1) In French: antipodaire. In German: Gegenfusspunktskurve.